[논문리뷰] ResNet (2016)

ResNet 논문 리뷰

논문: Deep Residual Learning for Image Recognition, Github
참고한 블로그

My Preview

Residual의 의미를 알아보자

A. 영어 단어 residual의 정의

• (adj.) remaining after the greater part or quantity has gone.
• (n.) a quantity remaining after other things have been subtracted or allowed for.

[출처: Oxford Languages]

즉 뭔가 “남아 있는” 것을 의미한다.

B. 통계학에서 residual이란

만약 모집단에서 회귀식을 얻었다면, 그 회귀식을 통해 얻은 예측값과 실제 관측값의 차이가 오차(error)이다.
반면 표본집단에서 회귀식을 얻었다면, 그 회귀식을 통해 얻은 예측값과 실제 관측값의 차이가 잔차(residual)이다.
둘의 차이는 모집단에서 얻은 것이냐 표본집단에서 얻은 것이냐 뿐이다.

[출처: https://bskyvision.com/642]

residual의 뜻으로 미루어보아 Deep Residual Learning이라는 건 딥러닝 모델에서 잔차(residual)를 이용하는 것으로 보인다.

0. Abstract

Neural Network가 깊어질수록 학습이 더 까다로워지는 점을 개선하기 위해 residual learning framework을 소개한다. Residual network를 활용하면 optimization이 쉬워지고, 모델을 깊게 구성하여 모델 성능을 높일 수 있다.

1. Introduction

Deep CNN을 통해 이미지 classification이 수월해지는 등, 모델이 깊어질수록 성능이 좋아진다는 것은 자명한 사실이다. 그래서 모델의 깊이를 따지다 보니 학습 초기부터 모델의 수렴을 방해하는 vanishing/exploding gradients 문제를 마주하게 됐다.

Deep network이 수렴하기 시작하면 모델 성능이 떨어지는 degradation 문제가 발생하게 되는데, 이는 overfitting에 의한 것이 아니며 이미 충분히 깊은 모델에 layer를 추가하게 되면 training error가 커진다. (overfitting일 경우엔 train acc는 높은데 test acc는 낮게 됨)

본 논문에서는 이러한 degradation 문제에 대한 해결책으로써 deep residual learning framework (=ResNet)을 소개한다. 각각의 쌓인 layer(each few stacked layers)가 underlying mapping(:=H(x), 다음 layer)에 fit하게 하는 게 아니라, residual mapping(F(x):=H(x)-x)에 fit하게 만들었다. 그러면 원래의 함수 H(x)는 F(x)+x로 다시 쓸 수 있다. 본 논문에서는 F(x)가 기존의 mapping인 H(x)보다 optimize하기 쉽다고 가정한다. 최선의 경우 identity mapping이 optimal하다면, nonlinear layers에 identity mapping을 fit하는 것보다 잔차(residual)를 0으로 만드는 것이 더 쉬울 것이다.

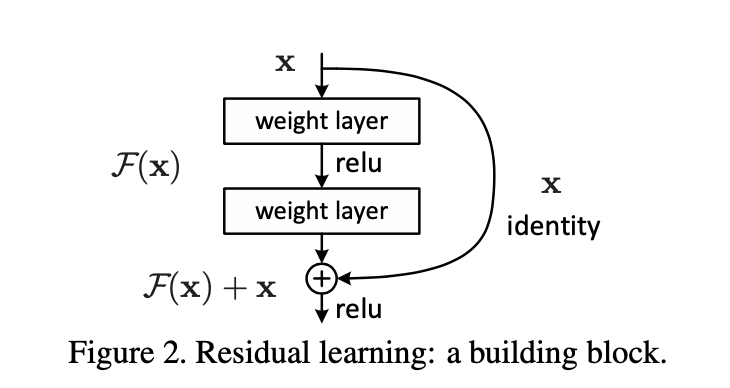
F(x)+x 공식은 “shortcut connections”를 가진 순방향 network(feedforward neural network)를 가지고 구현할 수 있다 (Fig. 2). Shortcut connections(=skip connection)이란 한 개 이상의 layer를 건너뛰는 것이다. 여기서 shortcut connection은 단순히 identity mapping을 수행하고, 이들의 output은 stacked layers의 output에 합쳐진다. Identity shortcut connection은 모델 파라미터를 새로 만들어내거나 연산을 복잡하게 만들지 않는다.

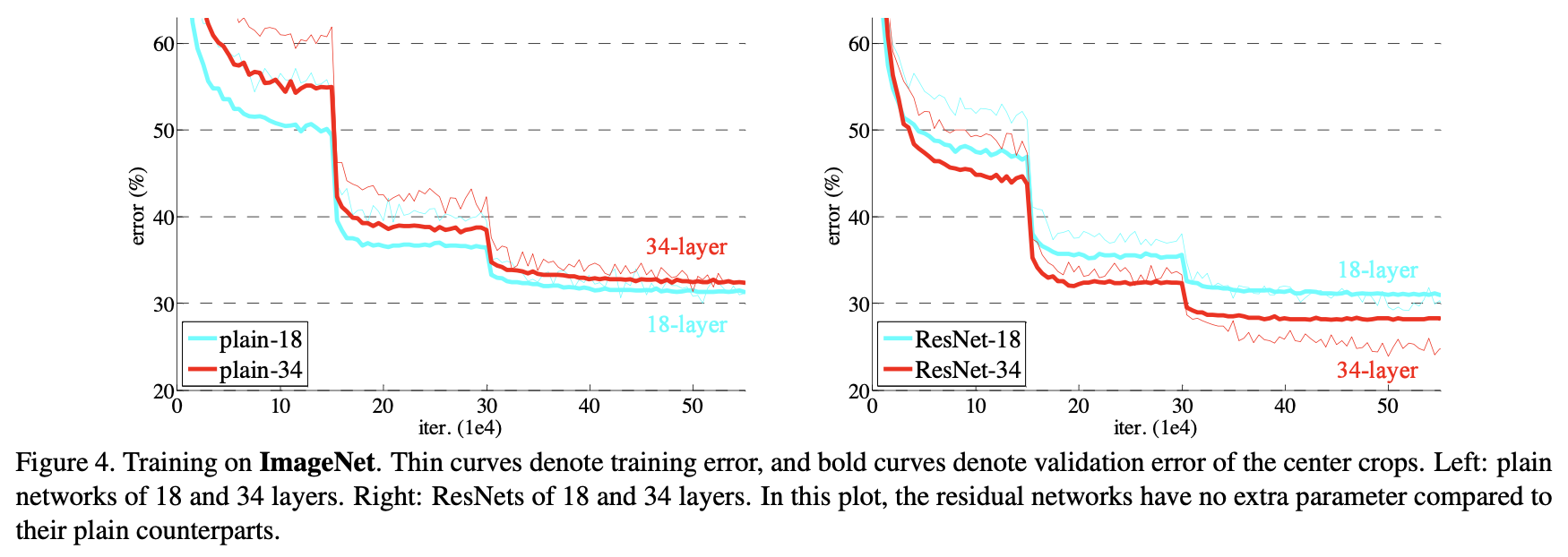
이 논문에서는 degradation 문제를 보이고 본 논문을 평가하기 위한 실험적인 방법들을 보여주고자 한다. 여기서는 (1) 단순히 layer를 쌓기만 하는 “plain” net은 깊이가 깊어질수록 training error가 커지는 반면, deep residual net은 optimize하기 좋다는 것을 보이고, (2) deep residual net를 더 깊게 함으로써 기존 모델들에 비해 상당히 좋은 결과를 보이면서 accuracy를 높일 수 있음을 보이고자 한다.

2. Related Work

대충 Residual Representations, Shortcut Connections 개념이 쓰였다 이런 얘기.

3. Deep Residual Learning

3.1. Residual Learning

쌓여있는 layer가 underlying mapping인 H(x)를 추정하게 하는 대신 residual function인 F(x):=H(x)-x를 추정하게 한다. 그럼 원래의 함수는 F(x)+x가 된다.
비록 두 식은 결국 형태만 다른 똑같은 식이지만 바뀐 형태만 가지고도 학습이 쉬워질 수 있다.

3.2. Identity Mapping by Shortcuts

본 논문에서는 모든 쌓여있는 layer에 대해 residual learning을 적용한다. 다음과 같은 building block을 고려한다.

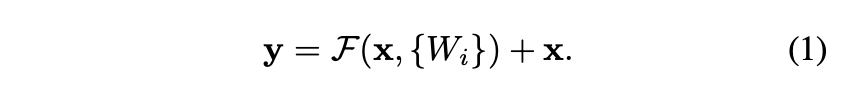
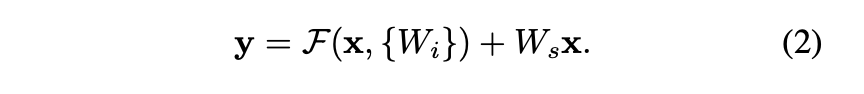
x와 y는 각각 layer의 input과 output 벡터를 의미한다. F(x, {Wi})는 학습 되어야 하는 residual mapping이다. F+x 연산은 shortcut connection과 element-wise addition (행렬 간 덧셈)을 통해서 수행된다. 덧셈 연산 다음에 second nonlinearity를 적용하게 된다. 이러한 shortcut connection은 모델 구조 및 연산을 복잡하게 만들지 않는다는 점에서 residual net을 차별화한다. (1)에서는 x와 F는 차원이 같아야 한다. 따라서 W1, W2 등의 linear projection을 통해 같은 차원으로 만들어줘야 한다. 이를 일반화한 공식이 (2)이다. 즉 (2)에서 Ws는 차원을 맞춰주는 용도로만 쓰인다.

3.3. Network Architectures

plain network과 residual network를 비교한다.

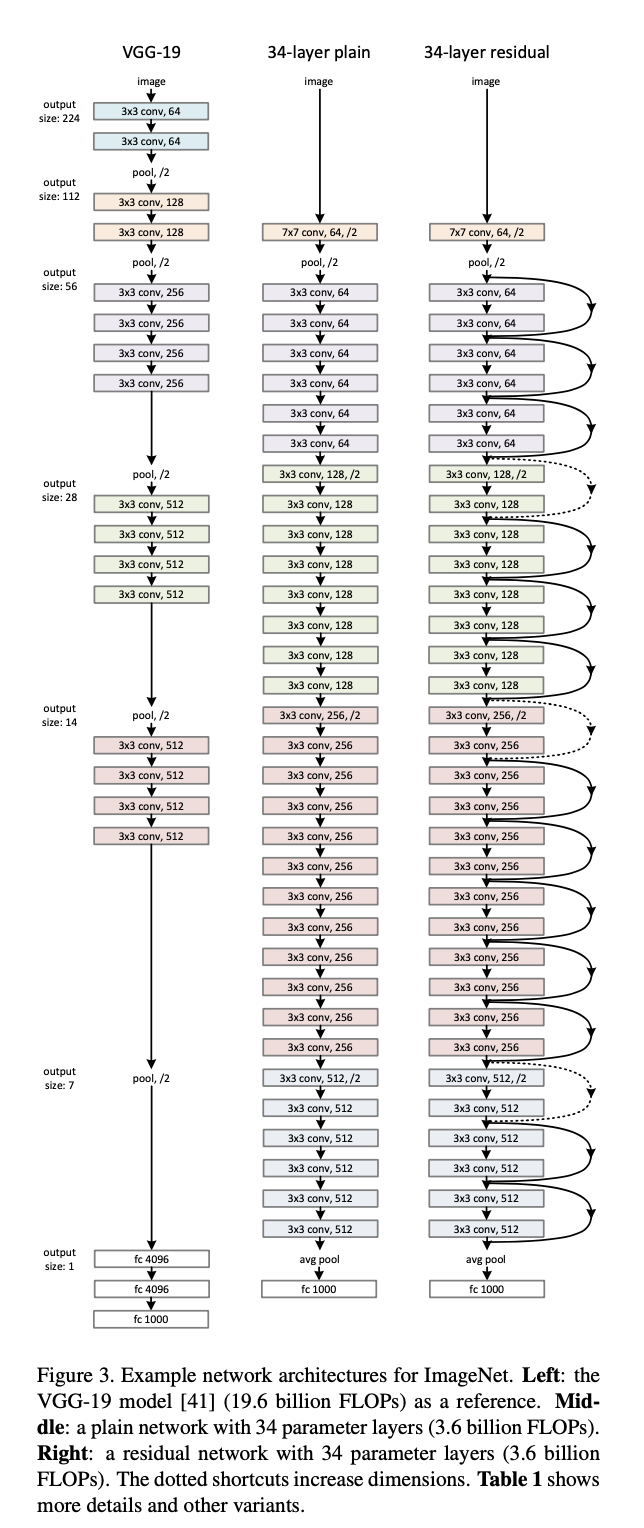
3.4. Implemention

• preprocessing
  • image resized with its shorter side randomly sampled in [256, 480] for scale augmentation.
  • 224x224 random crop from original image or its horizontal flip with centering (per-pixel mean subtracted)
  • standard color augmentation
• batch normalization (BN) right after convolution and before activation
• initialize weights
• SGD optimizer with a mini-batch size of 256
• learning rate 0.1
• 60x10^4 iterations
• weight decay 0.0001, momentum 0.9
• no dropout

4. Experiments

ResNet을 어떻게 평가했는지에 대해서 설명하고 있다.