[논문리뷰] Ranking Loss (2019, 2021)

Ranking Loss 관련 논문 리뷰

“Brain Age Estimation From MRI Using Cascade Networks With Ranking Loss” [1]에서 나온 Ranking Loss 개념 및 코드 이해해 보기.

chronological age (subject의 실제 나이)를 $y$, estimated brain age (뇌 나이 예측값)를 $\hat{y}$이라고 할 때, 두 데이터 샘플 간 관계 즉, age 간의 차이가 중요하다는 점을 이용하여 age difference loss를 (5)번 식과 같이 두 데이터의 estimated brain age difference와 true age difference에 대한 MSE로 나타낼 수 있다. ($ N_p $ : $ (i,j) $ 데이터 쌍의 개수)

$ L_d = \frac{1}{N_p} \sum_{(i,j)} ((\hat{y_i}-\hat{y_j})-(y_i-y_j))^2 $ (5)

이때 $L_d$가 두 샘플에 대한 ranking loss이다. age difference의 부호가 곧 두 개 age의 순서를 나타내기 때문이다. $L_d$는 age difference의 크기와 부호 모두 고려한다.

참고로 통계학에서 Spearman’s rank correlation coefficient (SRCC; 스피어만 상관계수)라는 게 있다.
Spearman 상관 계수는 두 변수의 유사 정도를 직관적으로 파악하기 위해 사용되는 도구로, rank variable의 Pearson 상관 계수를 계산하는 것으로 구할 수 있다. 그 식이 아래와 같다.

$ r_r = \frac{cov(Rank(\hat{y}), Rank(y))}{\sigma_{Rank(\hat{y})}\sigma_{Rank(y)}} $ (6)

$Rank$는 두 변수의 순서를 결정하는 rank operator이고, $cov(Rank(\hat{y}), Rank(y))$는 두 개의 rank variable에 대한 공분산 (covariance), $\sigma$는 각 rank variable에 대한 표준편차이다.
${\hat{y_i}}$와 ${y_i}$에서 각각 집합 안에 중복되는 값이 하나도 없으면 (6)번 식은 (7)번 식처럼 다시 쓸 수 있다. (${N}$: ${\hat{y_i}}$ 또는 ${y_i}$ 집합의 크기 = 총 데이터 수)

$ r_r = 1 - \frac{6\sum_i (Rank(\hat{y_i}) - Rank(y_i))^2}{N(N^2-1)} $ (7)

이 식에 대한 증명은 여기를 참고하면 된다.

참고로 만약 ${\hat{y_i}}$나 ${y_i}$에 중복 값이 있다면 rank operator는 fractional ranking operator가 된다.

cf. fractional ranking

데이터의 중복 횟수까지 고려해서 순위를 매기는 방식이다.
예를 들어 {1.0, 1.0, 2.0, 3.0, 3.0, 4.0, 5.0, 5.0, 5.0}이라는 데이터 집합이 있다고 하자.
그냥 순서대로 순위를 매기면 1~9까지가 될 텐데,
- 1, 2번 중복 (2개): (1+2)/2=1.5
- 4, 5번 중복 (2개): (4+5)/2=4.5
- 7, 8, 9번 중복 (3개): (7+8+9)/3=8.0
위와 같은 연산을 거쳐 순위 변수 집합이 {1.5, 1.5, 3.0, 4.5, 4.5, 6.0, 8.0, 8.0, 8.0}가 된다.

여기서 ranking loss를 중복 값이 없는 두 데이터 집합 간의 Spearman 상관계수를 가지고 정의하면 다음과 같다.

$ L_r = \sum_i (Rank (\hat{y_i}) - Rank (y_i))^2 $ (8)

${\hat{y_i}}$와 ${y_i}$ 집합 둘 다 중복 값이 없으면 (7)번 식을 따른다고 했는데, 그렇게 되면 $L_r$이 $1 - r_r$(1에서 Spearman 상관계수를 뺀 값)에 비례한다는 점에 주목하자.

(∵ (8)번 식을 (7)번 식에 대입하면 다음과 같이 됨.)

$ r_r = 1 - \frac{6L_r}{N(N^2 - 1)} $

$ L_r = \alpha * (1 - r_r) $, where $ \alpha = \frac{N(N^2-1)}{6} $

다시 말해서 $L_r$이 0에 가까울수록 Spearman 상관계수는 1에 가까워진다는 의미이고, 이는 곧 $L_r$ 값이 작을수록 예측값이 정답값에 근사하다는 것과 같다.
따라서 $L_r$ 값을 최소화하는 방향으로 학습 모델을 최적화하는 것이 이 논문의 주 목적이다.

한편 이렇게 Spearman 상관계수에 기반한 ranking loss는 gradient descent 최적화 알고리즘에 일반적으로 잘 쓰이는 기법은 아니다. gradient라는 건 기울기를 의미하기 때문에 미분 개념이 들어가게 되는데 ranking operator는 미분이 불가능하기 때문이다.

그런데 “SoDeep: A Sorting Deep Net to Learn Ranking Loss Surrogates” [2] 논문에서 rank variable을 미분할 수 있도록 수식을 조작해서 Spearman 상관계수에 기반한 ranking loss를 PyTorch로 구현한 게 있다. 친절하게 GitHub에 코드도 올라와 있다.

나는 이걸 내 연구에 적용해 볼 거라서 [2]를 읽으며 코드를 제대로 이해해 보기로 했다.

class SpearmanLoss(torch.nn.Module):
    """ Loss function  inspired by spearmann correlation.self
    Required the trained model to have a good initlization.
    Set lbd to 1 for a few epoch to help with the initialization.
    """
    def __init__(self, sorter_type, seq_len=None, sorter_state_dict=None, lbd=0):
        super(SpearmanLoss, self).__init__()
        self.sorter = model_loader(sorter_type, seq_len, sorter_state_dict)

        self.criterion_mse = torch.nn.MSELoss()
        self.criterionl1 = torch.nn.L1Loss()

        self.lbd = lbd

    def forward(self, mem_pred, mem_gt, pr=False):
        rank_gt = get_rank(mem_gt)

        rank_pred = self.sorter(mem_pred.unsqueeze(0)).view(-1)

        return self.criterion_mse(rank_pred, rank_gt) + self.lbd * self.criterionl1(mem_pred, mem_gt)

먼저 이건 Spearman Loss를 PyTorch Module로 구현한 클래스이다.

__init__ 메서드에서 보면 model_loader 함수를 이용하여 sorter를 불러오는데, 이 sorter가 rank variable를 미분 가능한 변수로 만들어주는 rank function의 surrogate이다.

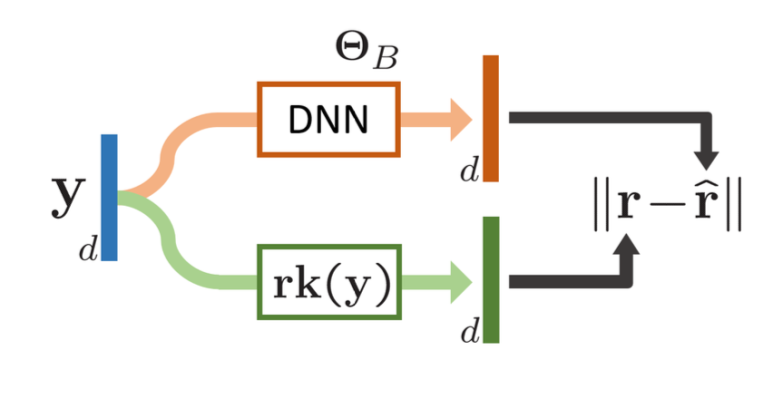
Training a differentiable sorter [2].
$\Theta_B$: learnable parameters of a DNN
$r$: rank from true rank vector ${rk(y)}$
$\hat{r}$: rank predicted from the DNN

위의 그림을 보면 이해가 쉽다.
d개의 데이터를 가진 y라는 벡터가 있고 y의 모든 원소에 대해 1부터 d까지 rank를 매긴 벡터를 ${rk(y)}$라고 할 때, 이 ${rk(y)}$를 예측하기 위한 sorter 모델 $f_{\Theta_B}$를 만든다.
즉 $f_{\Theta_B}$는 ranking operator의 역할을 하는 모델이고 이를 L1 loss를 가지고 학습시킴으로써 gradient descent를 최적화하고자 하는 것이다.

$ \min_{\Theta_B} \sum_{n=1}^N \Vert rk (y^{(n)}) - f_{\Theta_B} (y^{(n)}) \Vert_1 $ (${N}$: sample size)

sorter 네트워크는 그냥 단순한 convolutional architecture를 사용하고 있는데 이 부분에 대한 설명은 건너뛰겠다.

다시 코드로 돌아와서 코드에서 sorter는 이미 label 데이터에 대한 rank를 잘 매길 수 있다는 가정이 되어있기 때문에 pretrained model이어야 한다. 다행히 pretrained model 파일도 함께 제공되고 있어서 이걸 써보면 될 것 같다.
forward 메서드에서 보면 get_rank라는 메서드가 있는데 이건 이렇게 생겼다:

def get_rank(batch_score, dim=0):
    rank = torch.argsort(batch_score, dim=dim)
    rank = torch.argsort(rank, dim=dim)
    rank = (rank * -1) + batch_score.size(dim)
    rank = rank.float()
    rank = rank / batch_score.size(dim)

    return rank

[2]에서 구현한 rank operator는 위와 같은데, [1]에서 (내가 이해한 게 맞다면) 중복 값이 있을 것까지 고려해서 구현한 get_tiedrank 메서드도 있다.

def get_tiedrank(batch_score, dim=0):
    batch_score = batch_score.cpu()
    rank = stats.rankdata(batch_score)
    rank = stats.rankdata(rank) - 1    
    rank = (rank * -1) + batch_score.size(dim)
    rank = torch.from_numpy(rank).cuda()
    rank = rank.float()
    rank = rank / batch_score.size(dim)  
    return rank

get_rank나 get_tiedrank의 매개변수로는 ground truth가 들어가며 return 값은 ground truth의 rank이다.

SpearmanLoss를 loss function으로 쓰게 되면 이와 같이 rank operator를 이용한 ground truth의 rank인 $Rank(y_i)$와 sorter를 이용한 predicted rank $Rank(\hat{y_i})$ 간의 loss를 연산하는 것이다.

---

[1] Cheng, Jian, et al. “Brain age estimation from MRI using cascade networks with ranking loss.” IEEE Transactions on Medical Imaging 40.12 (2021): 3400-3412.
[2] Engilberge, Martin, et al. “Sodeep: a sorting deep net to learn ranking loss surrogates.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019.