[논문리뷰] LDS, FDS for Deep Imbalanced Regression (2021)

DIR 논문 & 코드 리뷰

논문: Delving into Deep Imbalanced Regression, Github, 저자의 포스트

My Preview

Imbalanced Regression

내가 학습에 사용하고 있는 데이터는 Medical data이다. Medical/Clinical/Healthcare data는 다른 데이터에 비해서 특히 더 불균형(imbalanced)인 경우가 많다. 일반적으로 질병을 예측하기 위한 건강 정보는 병에 걸린 사람보다 걸리지 않은 건강한 사람의 비율이 훨씬 높기 때문이다.
예를 들어 병변 데이터라고 하면 비교적 병변 수치가 작은 쪽으로 치우친 분포 형태인 right-skewed (positively skewed) distribution을 보이게 된다.

입력 데이터가 어떤 클래스에 속하는지를 알아보는 classification task에서의 imbalanced data handling에 대한 방법으로는 SMOTE(Synthetic Minority Oversampling Technique) 같은 것들이 알려져 있다.
그런데 내 연구 주제는 입력 데이터로 이미지를 주고 실수값을 예측하게 하는 regression task라서 SMOTE 같은 방법을 그대로 적용하기가 애매하다.

Delving into Deep Imbalanced Regression 논문에서는 이런 나에게 필요한 데이터 불균형 해결 방법을 소개하고 있다.

0. Abstract

기존의 데이터 불균형 문제를 해결하는 방식들은 범주형 데이터 (target with categorical indices)들의 불균형 문제에 초점을 맞추고 있다. (주로 classification task에서의 데이터 불균형) 본 논문에서는 연속적인 값들로 구성된 데이터를 학습할 때의 데이터 불균형 문제 (Deep Imbalanced Regression; DIR)를 해결할 수 있는 방법을 제시한다. 범주형 데이터와 연속형 데이터의 본질적인 차이점에서 착안하여 label과 feature에 대한 distribution smoothing 기법을 제안하고 있고, 이는 imbalanced regression problem에서 활용할 수 있다.

1. Introduction

데이터 불균형 문제는 편재한다. 이 현상은 기계 학습에도 큰 방해요소가 되기 때문에 이미 예전부터 이런 문제를 해결하는 방법들이 많이 제안되었다.

그러나 기존의 솔루션들은 일반적으로 이산적(discrete)으로 클래스(class)가 나뉘어 있는, 이른바 classification 문제에만 주력하고 있다. 정작 현실 세계의 데이터는 연속적이고 범위가 무한한 값들로 이뤄져 있으며 이러한 연속형 데이터 안에서도 불균형 문제가 있는 경우가 많다. 그 대표적인 예시가 내가 가지고 있는 것과 같은 medical/clinical data이다.

imbalanced regression은 imbalanced classification이 가지는 문제점과는 다른 문제점들이 있는데, 여기선 대표적으로 3가지를 들고 있다.

먼저 연속적인 타깃 값들은 (앞으로 타깃(target)이라고 하면 인공신경망 모델에 학습시킬 대상을 지칭한다.) 클래스 간 뚜렷한 경계가 없기 때문에 re-sampling이나 re-weighting 같은 전통적인 imbalanced classification 방식을 그대로 적용하기엔 애매해진다.
이게 무슨 말이냐 하면, 실수값 데이터는 classification으로 치면 그 값 자체로 하나의 클래스가 되어버린다. SMOTE 같은 re-sampling 기법은 보통 소수 클래스 샘플 사이사이에 임의의 값을 새로 생성하는 방식으로 이뤄지는데, 연속 데이터는 그 값 자체로 하나의 클래스니까 클래스 ‘사이사이’ 공간을 정의하기 매우 어려워지는 것이다.

방금 전 얘기와 같은 맥락에서 연속적인 타깃 데이터들은 타깃 값들 간 거리에도 의미가 있으며, 이건 데이터 불균형을 어떻게 해석해야 할지에 대한 힌트를 준다.
예를 들어서 training 데이터셋에서 t1, t2라는 두 개의 타깃이 있다고 해보자.

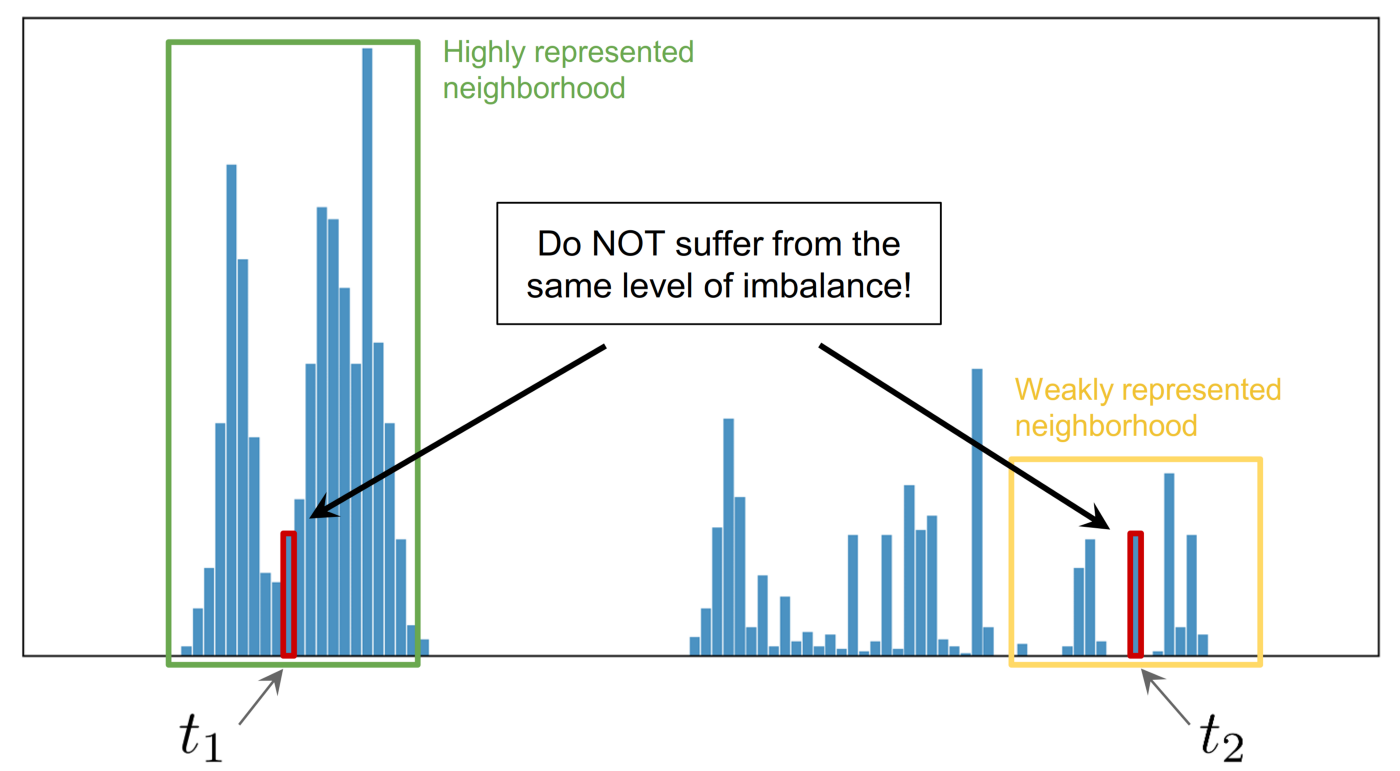
출처: 저자의 포스트
여기서 t1 주변의 값들은 빈도가 높은 반면 ([t1-∆, t1+∆] 범위 안에 샘플 수가 많음) t2는 그렇지가 않은 경우, 비록 t1의 개수와 t2의 개수가 같을지라도 두 타깃의 불균형 정도가 서로 같다고 할 수 없다.

마지막으로 classification과 달리, 어떤 타깃 값들은 데이터가 아예 존재하질 않아서 타깃의 extrapolation이나 interpolation을 필요로 한다.

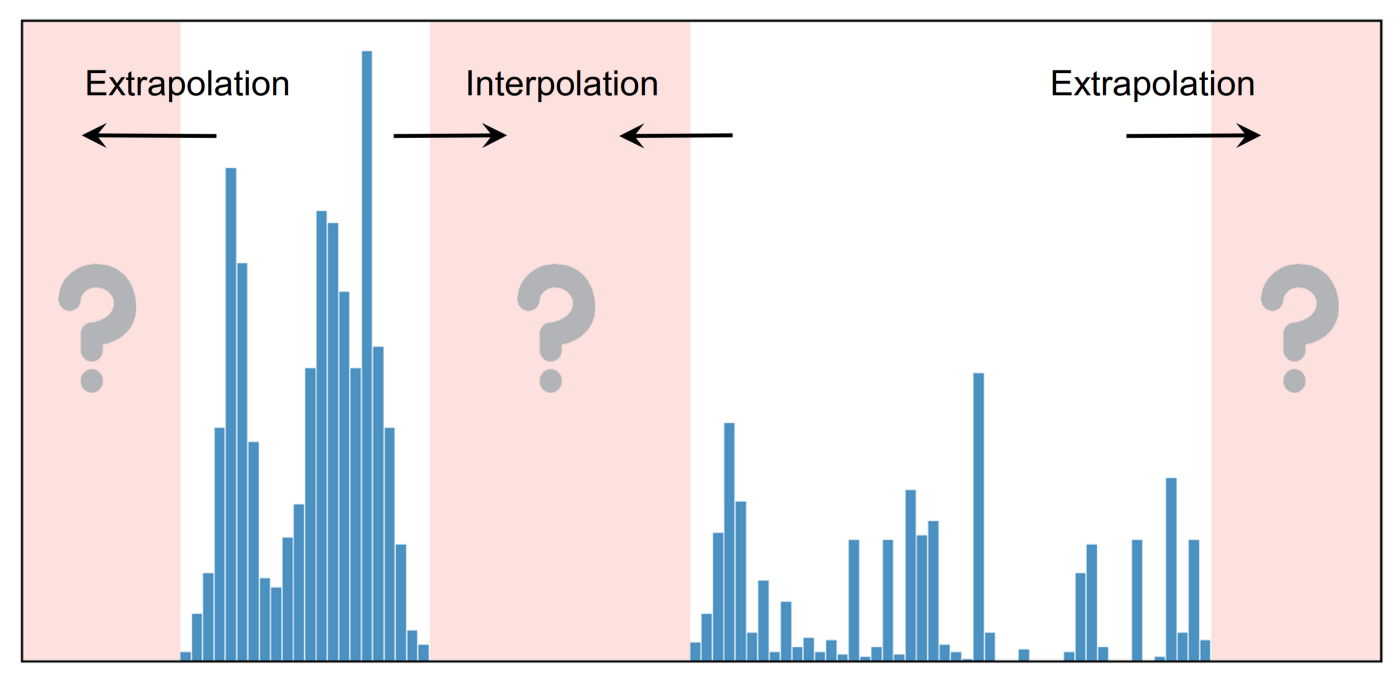
출처: 저자의 포스트

이 논문에서는 단순하면서도 효과적으로 DIR을 다루는 방법 두 가지를 선보인다: label distribution smoothing (LDS) and feature distribution smoothing (FDS). 두 접근법에 대한 핵심적인 발상은 kernel distribution을 활용해서 인접한 타깃들 간의 유사도 (similarity)를 이용함으로써 label space와 feature space 상에서 distribution smoothing을 해주는 것이다. 두 기술 모두 기존 딥러닝 모델들에 쉽게 적용할 수 있고 end-to-end 방식의 optimization이 가능하다. 또한 이 기술들은 다른 방법들을 함께 사용했을 때 더욱더 효과적이다.

2. Related work

대충 기존의 Imbalanced Classification (SMOTE 등등…), Imbalanced Regression (SMOTE 활용…) 과는 차별화 되었다는 이야기.

3. Methods

3.1. Label Distribution Smoothing

LDS 설명에 앞서 classification과 regression의 차이점에 대해서 예시를 가지고 설명한다.

Motivating Example.

label 범위가 0~99로 같고, label density distribution이 같은 classification 데이터셋과 regression 데이터셋을 가지고 설명해보겠다.
참고로 이 논문에서는 확실한 비교를 위해 두 데이터셋의 label density distribution을 인위적으로 똑같이 맞춰줬다.

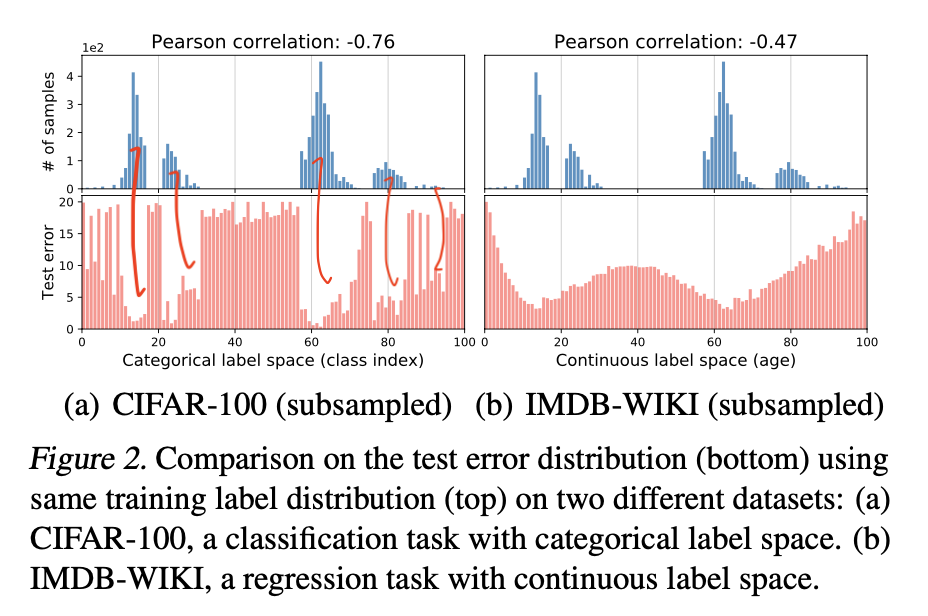
파란색 막대그래프로 표시된 위쪽 그림은 각 데이터셋의 분포를 보여주고, 빨간색 막대그래프로 표시된 아래쪽 그림은 학습 후의 label 별 test error를 나타낸다.
Figure 2.(a)를 보면 error distribution과 label density distribution에 negative correlation이 있음을 알 수 있다. 반면에 연속 데이터셋에 대한 그래프인 Figure 2.(b)를 보면 Figure 2.(a)에 비해서 error distribution이 훨씬 smooth하며 상대적으로 label density distribution과의 correlation이 없는 것으로 보인다.

일반적으로 re-weighting과 같은 imbalanced learning method는 실증적인 (empirical) label density distribution의 불균형에 가중치를 주는 식으로 작용한다. 이러한 방식은 test error distribution과 label density distribution 간의 correlation이 확실하게 보이는 클래스 데이터에 적용할 때는 효과적이지만, 연속적인 데이터에 대해선 테스트 에러가 실제 학습 모델에서 보이는 것만큼의 불균형을 제대로 반영하지 않기 때문에 그대로 적용하기에 적절치 않다.

LDS for Imbalanced Data Density Estimation.

앞선 예시에서 연속적인 데이터셋에 대해서는 empirical label density distribution이 실제 label density distribution을 반영하지 않는다는 것을 보였다. 이것은 인접한 label 데이터 샘플들 간의 의존성(dependence) 때문이다. 데이터 샘플 수가 부족하면 비교적 이웃한 값들 중에서 샘플 수가 높은 데이터에 의존하여 학습하게 되는 것이다.
Label Distribution Smoothing (LDS)는 이러한 문제를 해결하고 연속적인 타깃 데이터 간 불균형을 효과적으로 학습하기 위해 kernel density을 예측하는 방식이다.

LDS는 symmetric kernel과 empirical density distribution을 가지고 convolution을 해서 인접한 데이터 샘플 분포가 부드러워진 kernel-smoothed 버전을 만들어낸다. 즉 smoothing이라는 건 필터링 작업이다.
여기서 symmetric kernel이라는 건 k(y, y')=k(y', y)와 ∇y(k(y, y'))+∇y(k(y', y))=0, ∀y,y'∈Y (Y: label space)을 만족하는 모든 kernel을 의미한다. Gaussian kernel과 Laplace kernel은 symmetric kernel의 일종으로 볼 수 있고 k(y, y')=yy' 같은 건 symmetric kernel이 아니다. LDS는 결국 effective label density distribution을 다음과 같이 계산하게 된다:

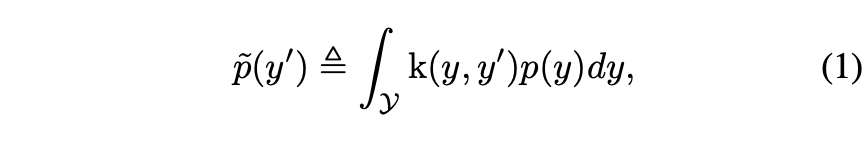
p(y)는 training data에서의 label 개수고, p~(y')는 y’ label의 effective density이다.

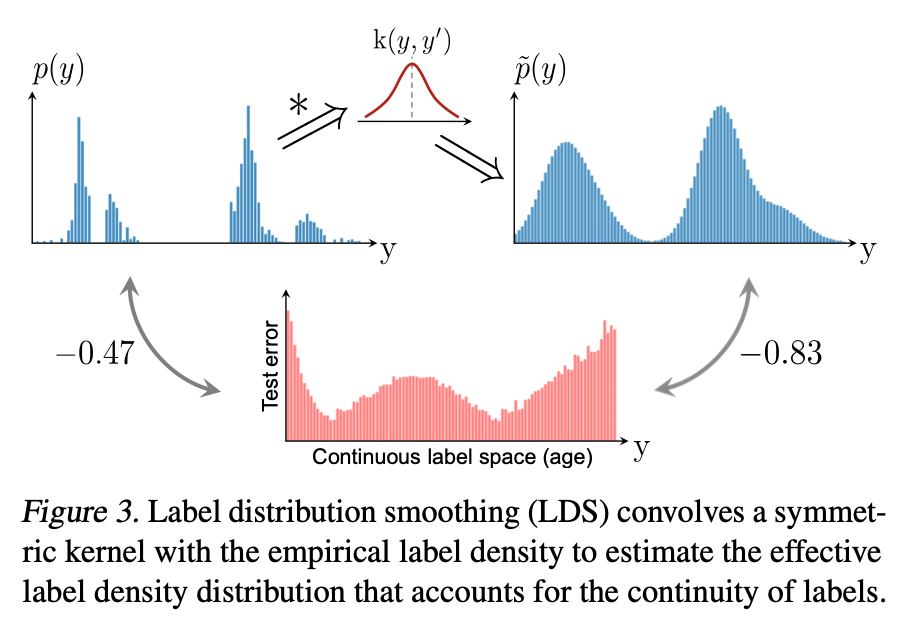
Figure 3은 LDS의 label density distribution 필터링 방식과 필터링 후 test error와의 correlation을 간단히 보여준다.

from scipy.ndimage import gaussian_filter1d
from scipy.signal.windows import triang
...

def get_lds_kernel_window(kernel, ks, sigma):
    assert kernel in ['gaussian', 'triang', 'laplace']
    half_ks = (ks - 1) // 2
    if kernel == 'gaussian':
        base_kernel = [0.] * half_ks + [1.] + [0.] * half_ks
        kernel_window = gaussian_filter1d(base_kernel, sigma=sigma) / max(gaussian_filter1d(base_kernel, sigma=sigma))
    elif kernel == 'triang':
        kernel_window = triang(ks)
    else:
        laplace = lambda x: np.exp(-abs(x) / sigma) / (2. * sigma)
        kernel_window = list(map(laplace, np.arange(-half_ks, half_ks + 1))) / max(map(laplace, np.arange(-half_ks, half_ks + 1)))

    return kernel_window

논문에서 제공하는 깃헙 레포에서 위의 LDS kernel을 생성하는 코드를 가져왔다.
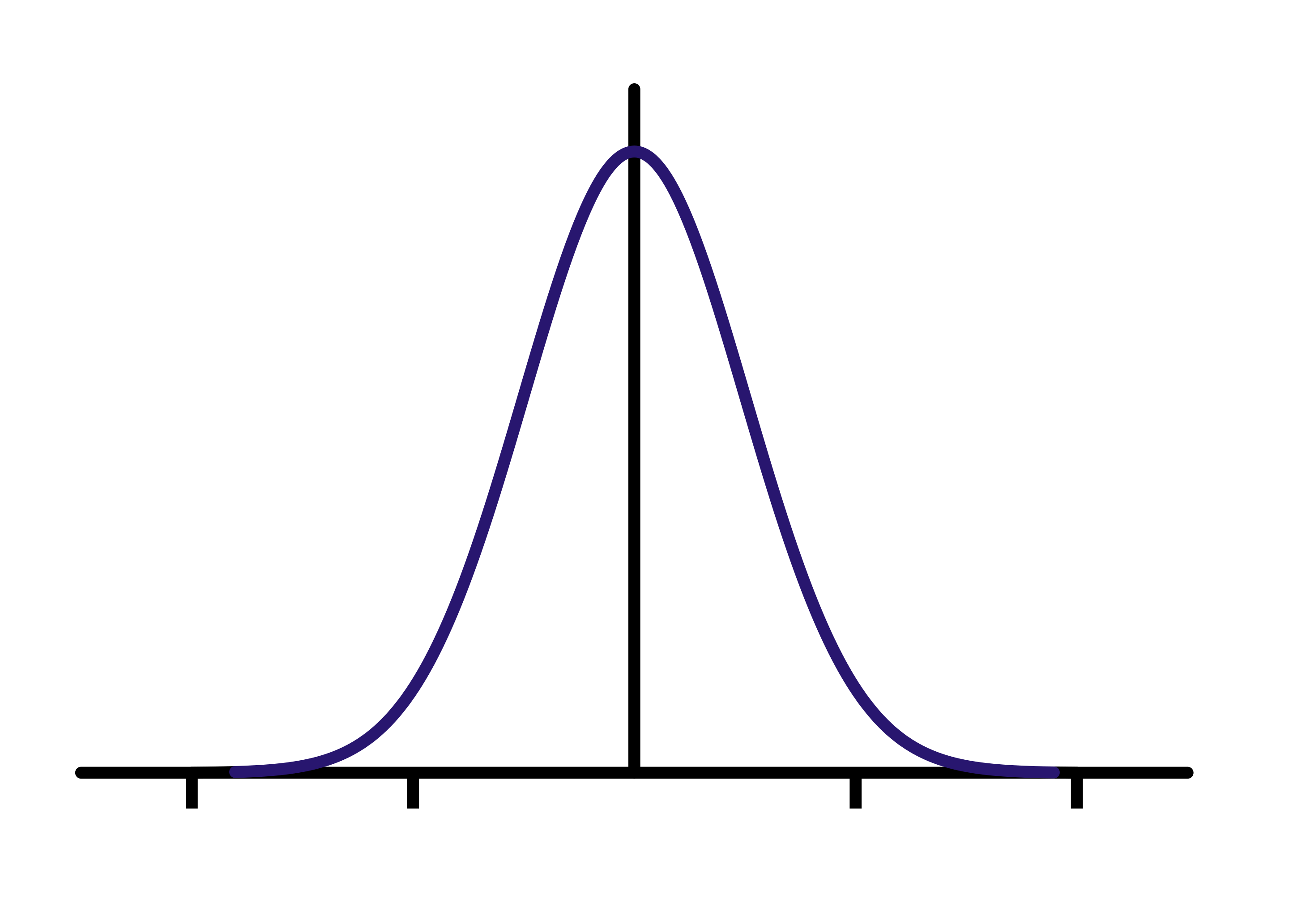
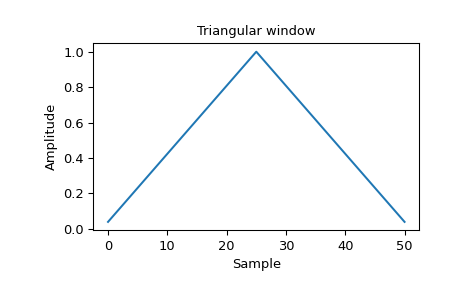
코드를 보면 위에서 symmetric kernel이라고 언급한 gaussian 필터와 laplace 필터를 구현하고 있다. triang은 triangle window, 즉 삼각형 필터이다. gaussian 필터와 삼각형 필터는 설명하지 않아도 그림을 보면 그냥 봐도 모두 symmetric(대칭)이라는 것을 알 수 있다:

출처: Wikipedia

출처: Scipy docs

laplace 필터는 discrete domain에서 쓰이는 필터로, 대충 이런 형태를 생각하면 된다:

출처: Wikipedia

즉 한가운데의 원소를 기준으로 대칭인 matrix이다.

그냥 내 생각
scipy.signal.windows에서는 삼각형 말고도 다양한 모양의 symmetric한 필터를 제공하고 있다.
커스터마이징을 위해 다른 필터들도 시도해볼 수 있을까?

LDS를 적용하는 방법은 다음과 같으며,

from collections import Counter
from scipy.ndimage import convolve1d
from utils import get_lds_kernel_window

# preds, labels: [Ns,], "Ns" is the number of total samples
preds, labels = ..., ...
# assign each label to its corresponding bin (start from 0)
# with your defined get_bin_idx(), return bin_index_per_label: [Ns,]
bin_index_per_label = [get_bin_idx(label) for label in labels]

# calculate empirical (original) label distribution: [Nb,]
# "Nb" is the number of bins
Nb = max(bin_index_per_label) + 1
num_samples_of_bins = dict(Counter(bin_index_per_label))
emp_label_dist = [num_samples_of_bins.get(i, 0) for i in range(Nb)]

# lds_kernel_window: [ks,], here for example, we use gaussian, ks=5, sigma=2
lds_kernel_window = get_lds_kernel_window(kernel='gaussian', ks=5, sigma=2)
# calculate effective label distribution: [Nb,]
eff_label_dist = convolve1d(np.array(emp_label_dist), weights=lds_kernel_window, mode='constant')

(bin index는 데이터 값들의 범위에 구간(bin)을 나눠서 구간마다 할당해주는 id라고 생각하면 된다.)

위에서 구한 effective label distribution 추정치를 가지고 loss re-weighting을 할 수 있다. 필터링을 통해 만들어진 smoothed label distribution이 좀 더 이상적인 데이터 분포라는 가정 하에, 원래의 정답 대신 이 분포에 맞춰서 loss 값을 계산하는 것이다. 코드 상으로는 loss function에 각 타깃에 LDS를 취한 label density 예측치의 역수를 곱해서 re-weighting을 함으로써 cost-sensitive하게 loss function을 re-weighting 하도록 구현되어 있다.

from loss import weighted_mse_loss

# Use re-weighting based on effective label distribution, sample-wise weights: [Ns,]
eff_num_per_label = [eff_label_dist[bin_idx] for bin_idx in bin_index_per_label]
weights = [np.float32(1 / x) for x in eff_num_per_label]

# calculate loss
loss = weighted_mse_loss(preds, labels, weights=weights)

def weighted_mse_loss(inputs, targets, weights=None):
    loss = (inputs - targets) ** 2
    if weights is not None:
        loss *= weights.expand_as(loss)
    loss = torch.mean(loss)
    return loss

3.2. Feature Distribution Smoothing

앞선 예시들을 통해 이제 target space에서의 연속성은 feature space에서의 연속성에 대응해야 함을 알 수 있다. 즉 학습 모델이 제대로 돌아가고 데이터 분포가 균형 잡혀 있다면, 인접 타깃에 대한 feature 통계를 봤을 때 인접한 애들끼리는 거의 유사한 feature를 뽑아낼 것이다.

Motivating Example.

예시로 학습된 feature의 통계를 분석해보려고 한다. 각 bin에 속한 타깃 데이터에 대한 평균(𝜇)과 표준편차(𝜎)를 계산한 것을 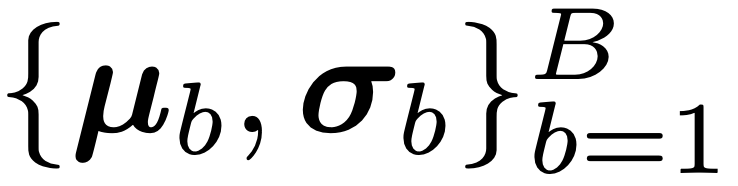라고 했을 때, (여기서 b는 타깃 값의 group index 또는 bin index를 나타낸다.) Figure 4는 타깃 값 30을 기준으로 (b 기준값 = 30) 각 타깃에 대한 feature 벡터 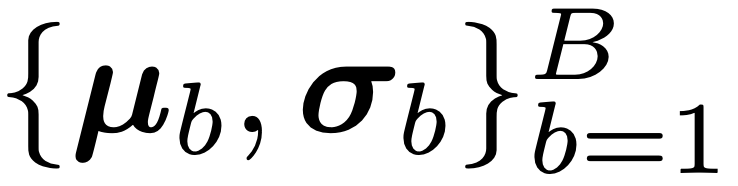의 코사인 유사도(cosine similarity)를 보여준다.

참고로 코사인 유사도는 두 벡터 간의 내적을 통해 두 벡터가 얼마나 비슷한지 계산하는 것이다. 유사도가 1에 가까울수록 유사한 것으로 볼 수 있고 -1에 가까우면 거의 유사하지만 방향만 반대인 것인데, 예제에서 다루고 있는 데이터는 사람의 나이 데이터라 양수 값만 있으므로 유사도 통계 역시 양수만 나올 것이다.
출처: 딥러닝을 이용한 자연어 처리 입문

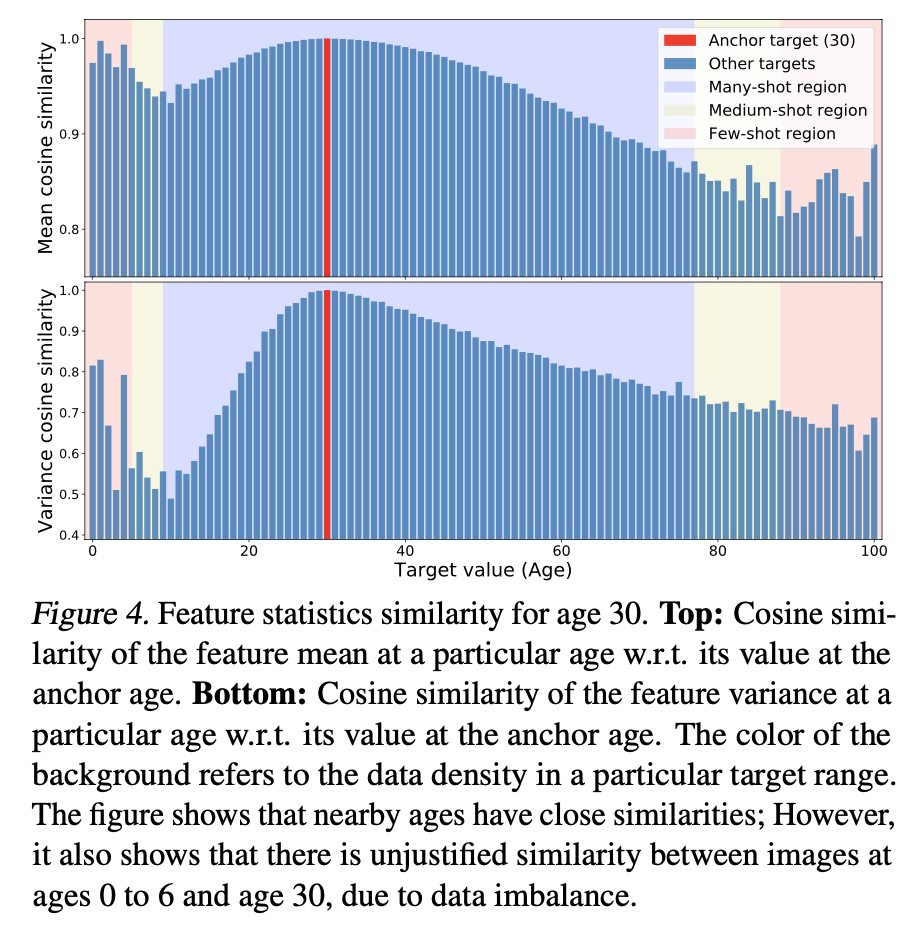
핑크색, 노란색, 파란색으로 표시된 곳은 차례대로 개수가 매우 적은 데이터, 개수가 보통인 데이터, 개수가 많은 데이터를 나타낸다. 위쪽의 평균 그래프에서 핑크색 구간 중에서도 특히 0~6 범위의 유사도가 거의 1인 것을 알 수 있다. 다시 말해서 0~6 범위 안에 있는 데이터가 충분히 많지 않다 보니 총 데이터 중 가장 많은 분포를 차지하는 대략 30에 가까운 값을 뱉어내는 것이다.

FDS Algorithm.

feature distribution smoothing (FDS)는 바로 이런 점에서 고안한 것이다.
FDS는 feature 벡터를 필터링 해서 편향된 feature 분포를 보정하는 것을 목표로 한다. 이말인즉슨 치우친 데이터, 특히 개수가 부족한 데이터의 예측치를 보정하겠다는 뜻이다.
먼저 feature space z에서 각 bin의 feature 평균 및 분산을 계산하고, 분산 값을 feature들의 covariance (공분산)으로 대치시켜서 feature 벡터를 정규화(normalize)한다.

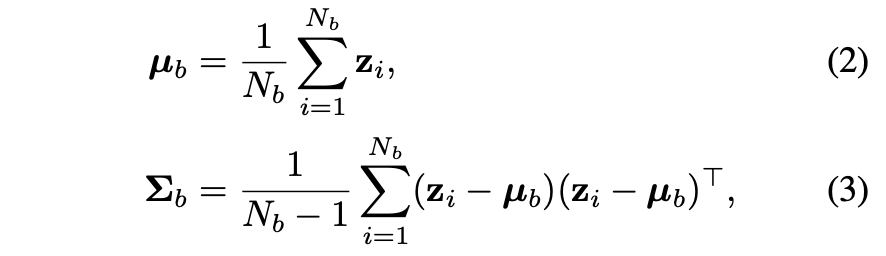
그리고 이렇게 바뀐 feature 벡터에 필터를 입힌다.

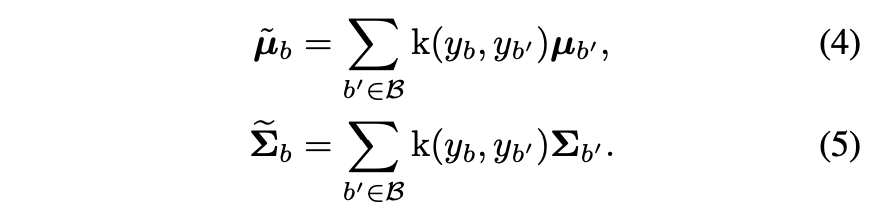
필터를 입히기 전의 {μb, Σb}와 {μ ̃b, Σb} 둘을 이용해서 standard whitening and re-coloring 절차를 거친다. (이 부분은 잘 모르는 개념이라서 해당 논문을 따로 정리해봐야 할 듯)

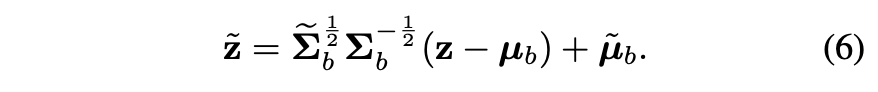
Figure 5는 이러한 과정을 집약적으로 표현한 것이다.

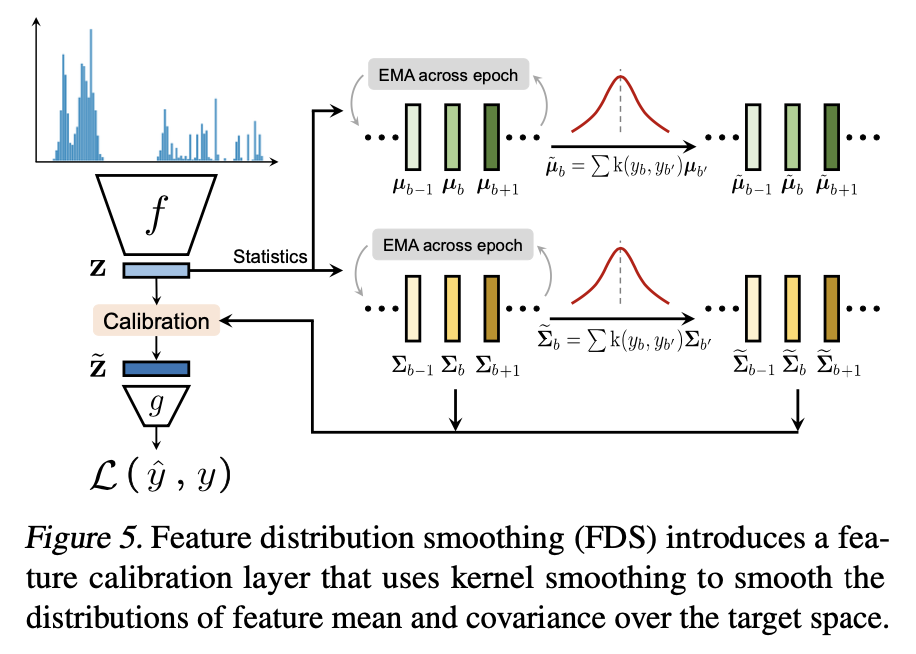
FDS는 마지막 feature map을 뽑아내는 layer 다음에 feature 보정 layer, 즉 FDS layer를 끼워넣는 방식으로 구현한다.

from fds import FDS

config = dict(feature_dim=..., start_update=0, start_smooth=1, kernel='gaussian', ks=5, sigma=2)

def Network(nn.Module):
    def __init__(self, **config):
        super().__init__()
        self.feature_extractor = ...
        self.regressor = nn.Linear(config['feature_dim'], 1)  # FDS operates before the final regressor
        self.FDS = FDS(**config)

    def forward(self, inputs, labels, epoch):
        features = self.feature_extractor(inputs)  # features: [batch_size, feature_dim]
        # smooth the feature distributions over the target space
        smoothed_features = features    
        if self.training and epoch >= config['start_smooth']:
            smoothed_features = self.FDS.smooth(smoothed_features, labels, epoch)
        preds = self.regressor(smoothed_features)

        return {'preds': preds, 'features': features}

학습을 할 때는 매 epoch마다 {𝜇b,𝛴b}의 momentum update를 해줌으로써 보다 안정적이고 정확하게 예측할 수 있다.

model = Network(**config)

for epoch in range(num_epochs):
    for (inputs, labels) in train_loader:
        # standard training pipeline
        ...

    # update FDS statistics after each training epoch
    if epoch >= config['start_update']:
        # collect features and labels for all training samples
        ...
        # training_features: [num_samples, feature_dim], training_labels: [num_samples,]
        training_features, training_labels = ..., ...
        model.FDS.update_last_epoch_stats(epoch)
        model.FDS.update_running_stats(training_features, training_labels, epoch)

4. Benchmarking DIR

이 논문에서 제안한 방법을 어떻게 시험했는지에 대해서 설명하고 있다.
IMDB-WIKI 데이터셋에서 bin 값은 0~7149 중에 있으며 validation 및 test set의 데이터 분포가 고르게끔 직접 구성하였다.

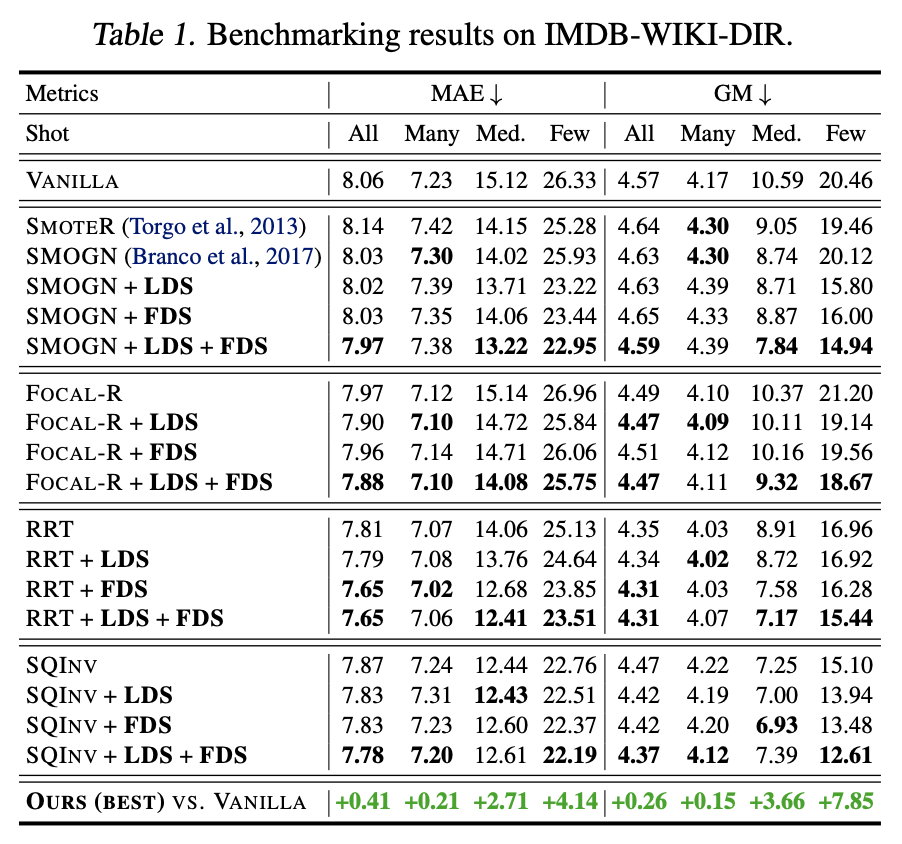
Table 1에서 Vanilla는 imbalance handling을 아예 안 한 것, Focal-R은 classification에서 쓰이는 Focal loss라는 loss 함수의 regression 버전, RRT는 feature와 classifier를 분리시켜서 두 단계로 나눠서 학습시키는 기법인 Two-stage training의 regression 버전이다. INV와 SQINV는 각각 inverse-frequency weighting variant, square-root weighting variant를 나타낸다.

저 표를 보면 LDS, FDS, 그리고 LDS랑 FDS를 둘 다 적용했을 때 아무것도 적용 안 했을 때보다 MAE가 작으므로 성능이 조금 더 좋아졌다고 볼 수 있다.